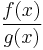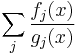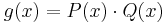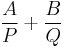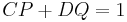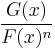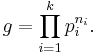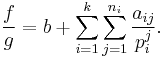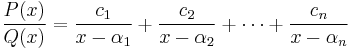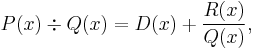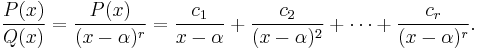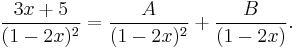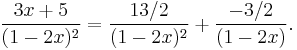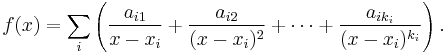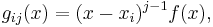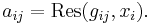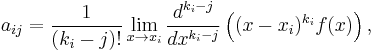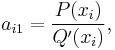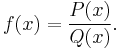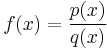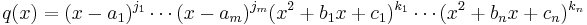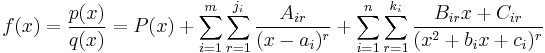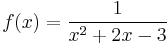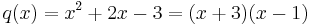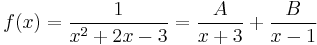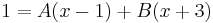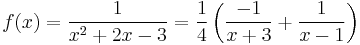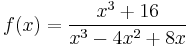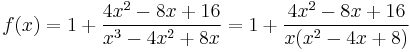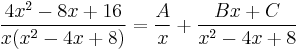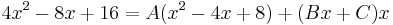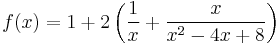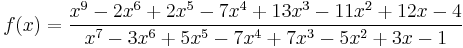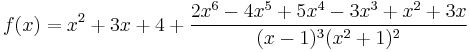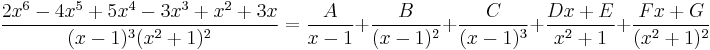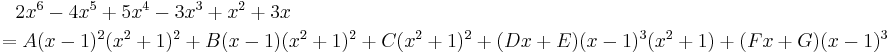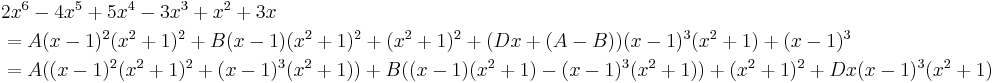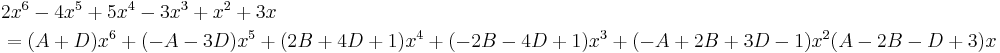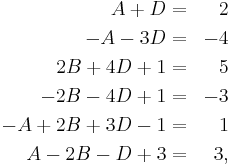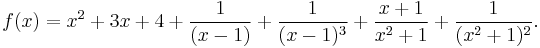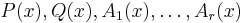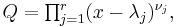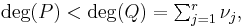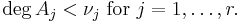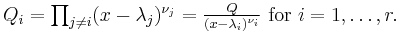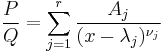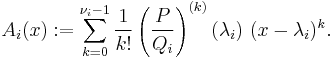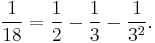Partial fraction
In algebra, the partial fraction decomposition or partial fraction expansion is a procedure used to reduce the degree of either the numerator or the denominator of a rational function (also known as a rational algebraic fraction).
In symbols, one can use partial fraction expansion to change a rational function in the form
where ƒ and g are polynomials, into a function of the form
where gj (x) are polynomials that are factors of g(x), and are in general of lower degree. Thus the partial fraction decomposition may be seen as the inverse procedure of the more elementary operation of addition of algebraic fractions, that produces a single rational function with a numerator and denominator usually of high degree. The full decomposition pushes the reduction as far as it will go: in other words, the factorization of g is used as much as possible. Thus, the outcome of a full partial fraction expansion expresses that function as a sum of fractions, where:
- the denominator of each term is a power of an irreducible (not factorable) polynomial and
- the numerator is a polynomial of smaller degree than that irreducible polynomial. To decrease the degree of the numerator directly, the Euclidean algorithm can be used, but in fact if ƒ already has lower degree than g this isn't helpful.
The main motivation to decompose a rational function into a sum of simpler fractions is that it makes it simpler to perform linear operations on it. Therefore the problem of computing derivatives, antiderivatives, integrals, power series expansions, Fourier series, residues, and linear functional transformations of rational functions can be reduced, via partial fraction decomposition, to making the computation on each single element used in the decomposition. See e.g. partial fractions in integration for an account of the use of the partial fractions in finding antiderivatives. Just which polynomials are irreducible depends on which field of scalars one adopts. Thus if one allows only real numbers, then irreducible polynomials are of degree either 1 or 2. If complex numbers are allowed, only 1st-degree polynomials can be irreducible. If one allows only rational numbers, or a finite field, then some higher-degree polynomials are irreducible.
Contents |
Basic principles
The basic principles involved are quite simple; it is the algorithmic aspects that require attention in particular cases. On the other hand, the existence of a decomposition of a certain kind is an assumption in practical cases, and the principles should explain which assumptions are justified.
Assume a rational function R(x) = ƒ(x)/g(x) in one indeterminate x has a denominator that factors as
over a field K (we can take this to be real numbers, or complex numbers). If P and Q have no common factor, then R may be written as
for some polynomials A(x) and B(x) over K. The existence of such a decomposition is a consequence of the fact that the polynomial ring over K is a principal ideal domain, so that
for some polynomials C(x) and D(x) (see Bézout's identity).
Using this idea inductively we can write R(x) as a sum with denominators powers of irreducible polynomials. To take this further, if required, write:
as a sum with denominators powers of F and numerators of degree less than F, plus a possible extra polynomial. This can be done by the Euclidean algorithm, polynomial case. The result is the following theorem:
Let ƒ and g be nonzero polynomials over a field K. Write g as a product of powers of distinct irreducible polynomials:
There are (unique) polynomials b and a ij with deg a ij < deg p i such that
If deg ƒ < deg g, then b = 0.
Therefore when the field K is the complex numbers, we can assume that each pi has degree 1 (by the fundamental theorem of algebra) the numerators will be constant. When K is the real numbers, some of the pi might be quadratic, so in the partial fraction decomposition a quotient of a linear polynomial by a power of a quadratic will occur. This therefore is a case that requires discussion, in the systematic theory of integration (for example in computer algebra).
Procedure
Given two polynomials 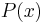 and
and 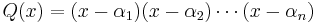 , where the αi are distinct constants and deg P < n, partial fractions are generally obtained by supposing that
, where the αi are distinct constants and deg P < n, partial fractions are generally obtained by supposing that
and solving for the ci constants, by substitution, by equating the coefficients of terms involving the powers of x, or otherwise. (This is a variant of the method of undetermined coefficients.)
This approach does not account for several other cases, but can be modified accordingly:
- If deg P
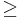 deg Q, then it is necessary to perform the division
deg Q, then it is necessary to perform the division
-
- via polynomial long division or otherwise, and then seek partial fractions for the remainder fraction (which by definition has deg R < deg Q).
- If Q(x) contains factors which are irreducible over the given field, then the numerator N(x) of each partial fraction with such a factor F(x) in the denominator must be sought as a polynomial with deg N < deg F, rather than as a constant. For example, take the following decomposition over R:
- Suppose Q(x) = (x − α)rS(x) and S(α) ≠ 0. Then Q(x) has a zero α of multiplicity r, and in the partial fraction decomposition, r of the partial fractions will involve the powers of (x − α). For illustration, take S(x) = 1 to get the following decomposition:
Illustration
In an example application of this procedure, (3x + 5)/(1 − 2x)2 can be decomposed in the form
Clearing denominators shows that 3x + 5 = A + B(1 − 2x). Expanding and equating the coefficients of powers of x gives
- 5 = A + B and 3x = −2Bx
Solving for A and B yields A = 13/2 and B = −3/2. Hence,
Residue method
Over the complex numbers, suppose ƒ(x) is a rational proper fraction, and can be decomposed into
Let
then according to the uniqueness of Laurent series, aij is the coefficient of the term (x − xi)−1 in the Laurent expansion of gij(x) about the point xi, i.e., its residue
This is given directly by the formula
or in the special case when xi is a simple root,
when
Note that P(x) and Q(x) may or may not be polynomials.
Over the reals
Partial fractions are used in real-variable integral calculus to find real-valued antiderivatives of rational functions. Partial fraction decomposition of real rational functions is also used to find their Inverse Laplace transforms. For applications of partial fraction decomposition over the reals, see
General result
Let ƒ(x) be any rational function over the real numbers. In other words, suppose there exist real polynomials p(x) and q(x)≠ 0, such that
By removing the leading coefficient of q(x), we may assume without loss of generality that q(x) is monic. By the fundamental theorem of algebra, we can write
where a1,..., am, b1,..., bn, c1,..., cn are real numbers with bi2 - 4ci < 0, and j1,..., jm, k1,..., kn are positive integers. The terms (x - ai) are the linear factors of q(x) which correspond to real roots of q(x), and the terms (xi2 + bix + ci) are the irreducible quadratic factors of q(x) which correspond to pairs of complex conjugate roots of q(x).
Then the partial fraction decomposition of ƒ(x) is the following:
Here, P(x) is a (possibly zero) polynomial, and the Air, Bir, and Cir are real constants. There are a number of ways the constants can be found.
The most straightforward method is to multiply through by the common denominator q(x). We then obtain an equation of polynomials whose left-hand side is simply p(x) and whose right-hand side has coefficients which are linear expressions of the constants Air, Bir, and Cir. Since two polynomials are equal if and only if their corresponding coefficients are equal, we can equate the coefficients of like terms. In this way, a system of linear equations is obtained which always has a unique solution. This solution can be found using any of the standard methods of linear algebra.
Examples
Example 1
Here, the denominator splits into two distinct linear factors:
so we have the partial fraction decomposition
Multiplying through by x2 + 2x - 3, we have the polynomial identity
Substituting x = -3 into this equation gives A = -1/4, and substituting x = 1 gives B = 1/4, so that
Example 2
After long-division, we have
Since (−4)2 − 4(8) = −16 < 0, x2 − 4x + 8 is irreducible, and so
Multiplying through by x3 − 4x2 + 8x, we have the polynomial identity
Taking x = 0, we see that 16 = 8A, so A = 2. Comparing the x2 coefficients, we see that 4 = A + B = 2 + B, so B = 2. Comparing linear coefficients, we see that −8 = −4A + C = −8 + C, so C = 0. Altogether,
The following example illustrates almost all the "tricks" one would need to use short of consulting a computer algebra system.
Example 3
After long-division and factoring, we have
The partial fraction decomposition takes the form
Multiplying through by (x − 1)3(x2 + 1)2 we have the polynomial identity
Taking x = 1 gives 4 = 4C, so C = 1. Similarly, taking x = i gives 2 + 2i = (Fi + G)(2 + 2i), so Fi + G = 1, so F = 0 and G = 1 by equating real and imaginary parts. With C = G = 1 and F = 0, taking x = 0 we get A - B + 1 - E - 1 = 0, thus E = A - B.
We now have the identity
Expanding and sorting by exponents of x we get
We can now compare the coefficients and see that
with A = 2 - D we get A = D = 1 and so B = 0, furthermore is C = 1, E = A - B = 1, F = 0 and G = 1.
The partial fraction decomposition of ƒ(x) is thus
The role of the Taylor polynomial
The partial fraction decomposition of a rational function can be related to Taylor's theorem as follows. Let
be real or complex polynomials; assume that
that
and that uyu
Define also
Then we have
if, and only if, for each 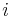 the polynomial
the polynomial 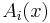 is the Taylor polynomial of
is the Taylor polynomial of 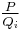 of order
of order 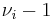 at the point
at the point 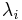 :
:
Taylor's theorem (in the real or complex case) then provides a proof of the existence and uniqueness of the partial fraction decomposition, and a characterization of the coefficients.
Sketch of the proof: The above partial fraction decomposition implies, for each 1 ≤ i ≤ r, a polynomial expansion
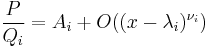 , as
, as 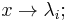
so 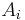 is the Taylor polynomial of
is the Taylor polynomial of 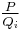 , because of the unicity of the polynomial expansion of order
, because of the unicity of the polynomial expansion of order 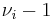 , and by assumption
, and by assumption 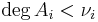 .
.
Conversely, if the 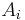 are the Taylor polynomials, the above expansions at each
are the Taylor polynomials, the above expansions at each 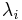 hold, therefore we also have
hold, therefore we also have
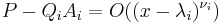 , as
, as 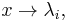
which implies that the polynomial 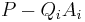 is divisible by
is divisible by 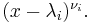
For 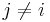 also
also 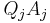 is divisible by
is divisible by 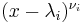 , so we have in turn that
, so we have in turn that 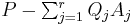 is divisible by
is divisible by 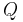 . Since
. Since 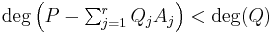 we then have
we then have 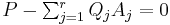 , and we find the partial fraction decomposition dividing by
, and we find the partial fraction decomposition dividing by 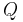 .
.
Fractions of integers
The idea of partial fractions can be generalized to other rings, say the ring of integers where prime numbers take the role of irreducible denominators. E.g., it is:
Notes
References
- Kudryavtsev, L.D. (2001), "Undetermined coefficients, method of", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=u/u095160.
- Charles D. Miller, Margaret L. Lial, David I. Schneider: Fundamentals of College Algebra. Scott & Foresman/Little & Brown Higher Education, 3rd edition 1990, ISBN 0-673-38638-4, p. 364-370
External links
- Weisstein, Eric W., "Partial Fraction Decomposition" from MathWorld.
- [1] Make partial fraction decompositions with Scilab.